Rögzítsünk fehér papírlapot rajztáblára, és állítsunk síktükröt (zsebtükör) a papírra merőlegesen! Szúrjunk le két gombostűt a táblába (, A, B pont), és a rajztáblát szemmagasságba emelve, egy szemmel nézzünk a két gombostű vonalába, majd keressük meg egy harmadik gombostűvel azt a C pozíciót, amelybe a leszúrt gombostűről jövő fénysugár a tükörről visszaverődve az AB egyenesbe esik! Szúrjuk le a negyedik gombostűt is (D) úgy, hogy a négy gombostűt az AB irányból nézve egy vonalban lássuk! Rajzoljuk le a tükör helyzetét és a két-két gombostűt összekötő egyeneseket a papírra! A rajzról igazolható a beesési és a visszaverődési szög egyenlősége.
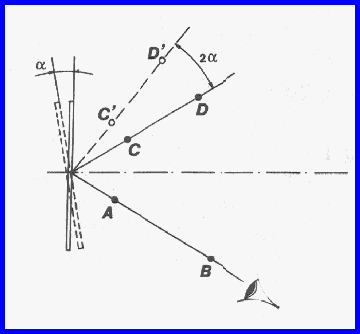
Ismételjük meg a kísérletet úgy is, hogy a tükröt, korábbi helyzetéhez képest a szöggel elforgatjuk! Igazoljuk a fenti módon újabb két gombostű leszúrásával, hogy a visszavert fénysugár elfordulási szöge 2a!

Megjegyzések

• A geometriai optika alapkísérletei, mérései egyszerűen elvégezhetők gombostűkísérletekkel. Ezek közös alapja az, hogy a természetes megvilágítás diffúz fényéből kiválaszthatunk egy-egy fénysugarat két letűzött gombostű segítségével.
• Ha a vízszintes rajztáblába beszúrt két gombostűt egy szemmel úgy nézzük, hogy a két tű egymást fedni látszik, akkor szemünk pontosan a két gombostűvel meghatározott fénysugár irányába néz. Ezt az irányt a két gombostű közé húzott vonallal a rajztáblán lévő papírra rögzíteni lehet. Ha az így kitűzött fénysugár útjába tükröt, prizmát plánparalel lemezt helyezünk, amely a fénysugár útját megváltoztatja, akkor újabb, az előzőekkel fedésben látszó gombostűkkel ez az irány is rögzíthető, és a papírra átrajzolható. Az így készített ábra tulajdonképpen egy kísérleti úton végzett szerkesztési rajz, amiről a geometriai optika törvényei kiolvashatók.